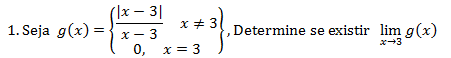
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que: Como os limites laterais quando x se aproxima de 3 são diferentes então não existe limite Quando x se aproxima de 3
Como os limites laterais quando x se aproxima de 3 são diferentes então não existe limite Quando x se aproxima de 3
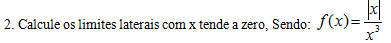
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que:
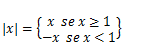
Então a nossa função fica ;
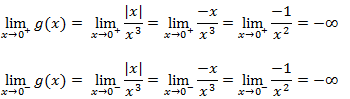
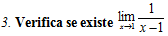
Calculemos os limites laterais

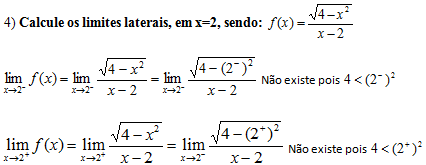
5) Calcular os limites.
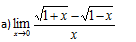
Primeiro vamos Substituir onde vem x pela tendência que é 0
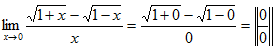
Temos uma indeterminação do tipo zero sobre zero 0/0 para resolver este limite (para levantar a indeterminação) devemos recorrer ao par conjugado da expressão que conte a raiz (do numerador)
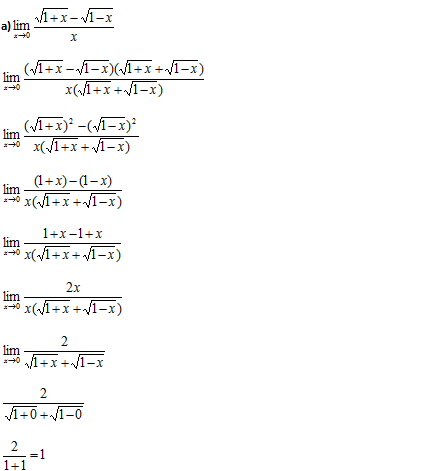
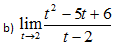
Primeiro vamos Substituir onde vem t pela tendência que é 2
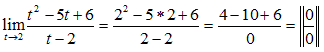
Para levantar a indeterminação devemos fautorizar
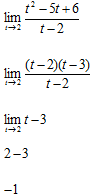
Primeiro vamos Substituir onde vem x pela tendência que é 2
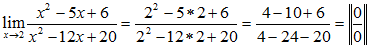
Para levantar a indeterminação devemos fautorizar
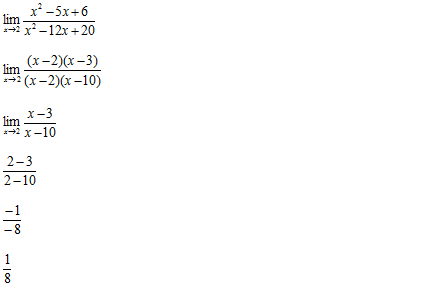
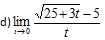
Primeiro vamos Substituir onde vem t pela tendência que é 0
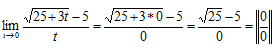
Temos uma indeterminação do tipo zero sobre zero 0/0 para resolver este limite (para levantar a indeterminação) devemos recorrer ao par conjugado da expressão que conte a raiz (do numerador)
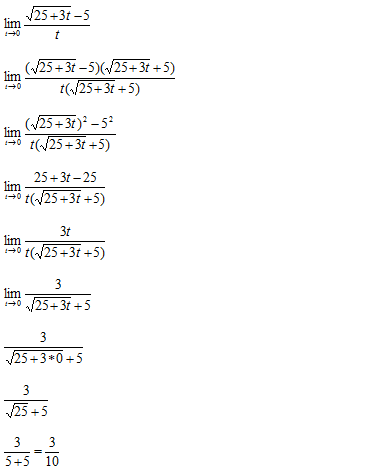
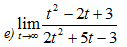
Para resolver esse limite como t tende papa infinito vamos simplesmente levar o termo de maior grão do numerado e denominador
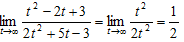
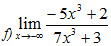
Para resolver esse limite como x tende papa menos infinito vamos levar o termo de maior grão do numerado e denominador
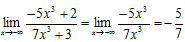
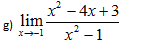
Primeiro vamos Substituir onde vem t pela tendência que é -1
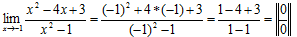
Para levantar a indeterminação vamos factorizar
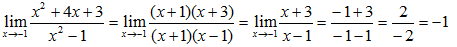
6) Explicite, os pontos de descontinuidade das seguintes funções:
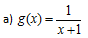
Primeiro vamos calcular o domínio
x+1≠0
x≠-1
Como -1 não faz parte do domínio a função e descontinua em x=-1
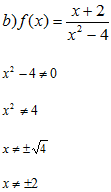
Como -2 e 2 não fazem parte do domínio a função e descontinua em x=-2 e x=27) Verificar, através da definição, a continuidade ou descontinuidade (em x = 4) da função:
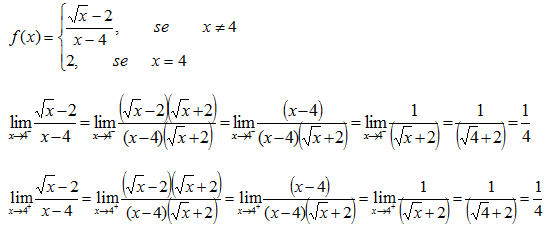
8) Determinar, através da definição de continuidade, todos os valores de x para os quais a função abaixo não é contínua.
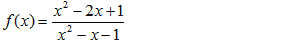
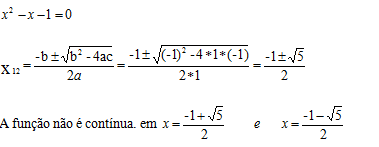
11) Explique por que a função é descontínua em x=1.
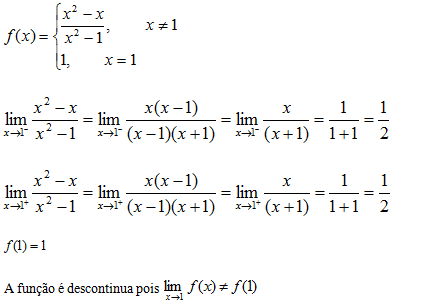
Depois dessa aula veja Resolução de (Teste I) de Calculo I UNIFEI
12) Determine as assíntotas verticais e horizontais (se existirem) das funções abaixo:







13) Relacione cada limite da função g(x) com um dos gráficos abaixo:
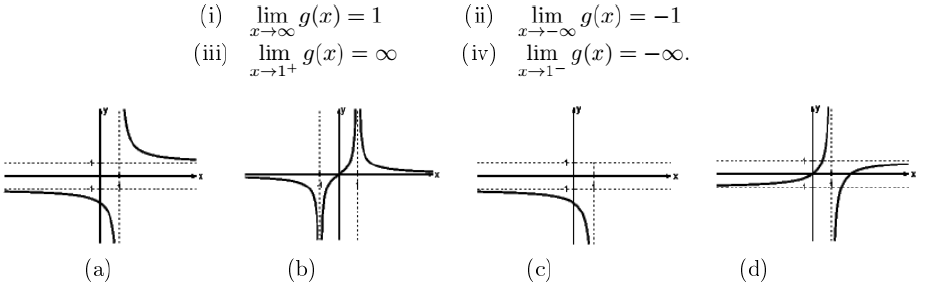
(I): (a),(d)
(II): (a),(c), (d)
(III): (a),(b)
(IV): (a),(c
©Exercícios elaborados por Instituto federal goiano
Resolução de (Teste I) de Calculo I UNIFEI
Resolução de exercícios sobre limites trigonométricos
Uma vez que já vimos o limite trigonométrico fundamental a gora e a hora de usar esse conh…
Limites trigonométricos
Para resolver exercícios de limites trigonométricos devemos antes conhecer e ter o domínio…
Limite notável (limite exponencial)
O Limite notável é base para a resolução de diversos limites exponencial é praticamente impossível r…
Limite exponencial (limite de Euler)
Limite exponencial são conhecido vulgarmente como limite de Euler, a indeterminação nos li…
Limites indeterminações do tipo zero sobre zero
Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a var…
Limites indeterminações do tipo infinito sobre infinito
Limites contendo indeterminações do tipo infinito sobre infinito são limites&nbs…






