Teoremas de integrais de contorno
Teorema 1. Integral de Cauchy
Seja uma função f(z) analítica numa região conexa R e seja г um contorno fechado simples, todo contido em R.
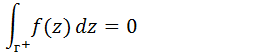
Teorema 2. Formula de integral de Cauchy
Seja uma função f(z) analítica em todos pontos contidos em um contorno г , e z₀ um ponto também contido no contorno г ;
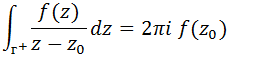
Teorema 3. integral de contorno
Sendo f(z) uma função analítica em todos pontos situados no interior de um contorno fechado simples , f(z) possui derivadas de todas ordens em qualquer ponto z₀ interior a г e pode ser encontrado a partir de;
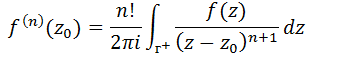
Podemos isolar a integral, e fazendo isto temos;
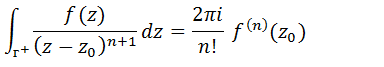
Exercícios resolvidos sobre integral de contorno (variável complexa)
Calcule a integral de;
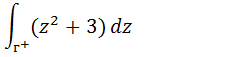
Nesse caso o nosso f(z) é z²+3 e de acordo com a formula de Cauchy essa integral da zero
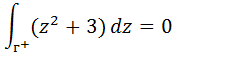
2.Integrais de contorno Exercício #2 Calcule a integral
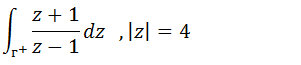
Comparando a nossa forma com a forma da integral de Cauchy podemos notar que;
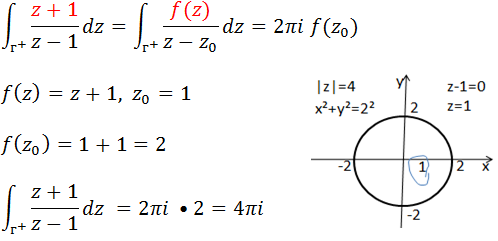
3.Integrais de contorno Exercício #3 Calcule a integral de Cauchy
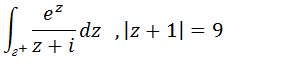
Vamos desenhar a região
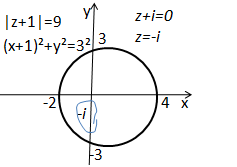
Comparando a nossa forma com a forma da integral de Cauchy podemos notar que;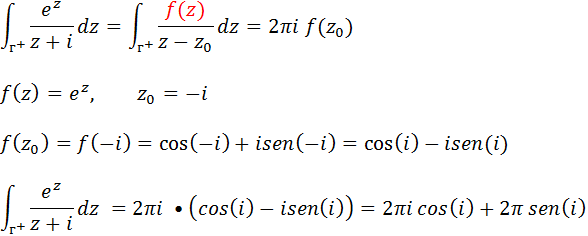
4.Integrais de contorno Exercício #4 Calcule a integral de Cauchy;
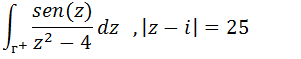
Primeiro vamos representar o contorno
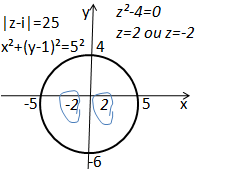
Comparando a nossa forma com a forma da integral de Cauchy podemos notar que;
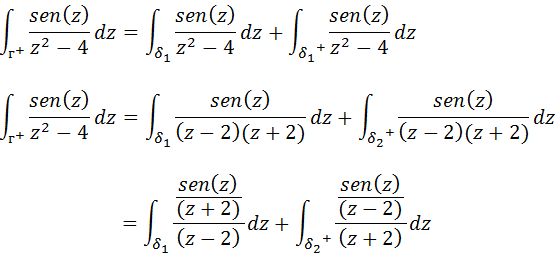
Vamos calcular a primeira integral
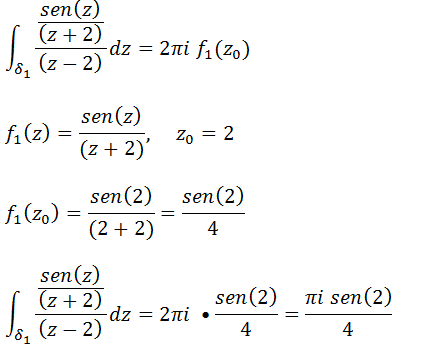
Vamos agora calcular a segunda integral
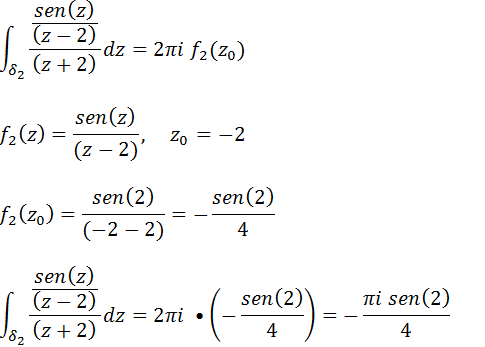
Vamos somas os resultados da integral 1 e 2 de modo a encontrar o resultado final da nossa integral de contorno.
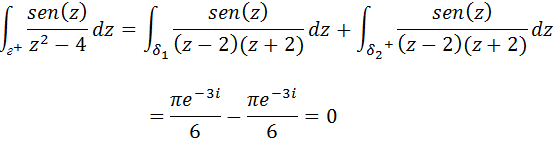
5.Integrais de contorno Exercício #5 Calcule a integral de Cauchy
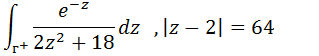
vamos desenhar a região
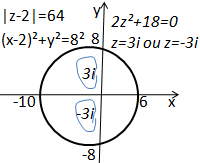
Vamos evidenciar o dois no denominador
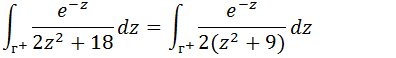
Vamos fazer algumas articulações de modo a termos uma expressão idêntica a da integra de Cauchy (passar o dois para o numerador da expressão principal)
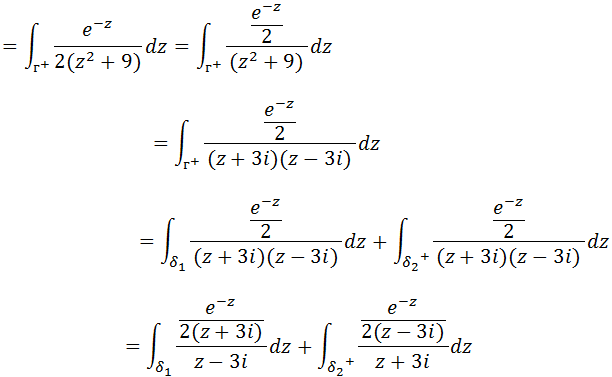
Vamos calcular a primeira integral
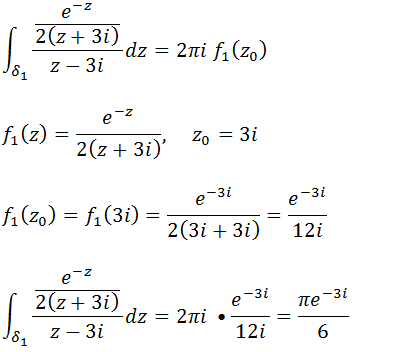
Vamos agora calcular a segunda integral
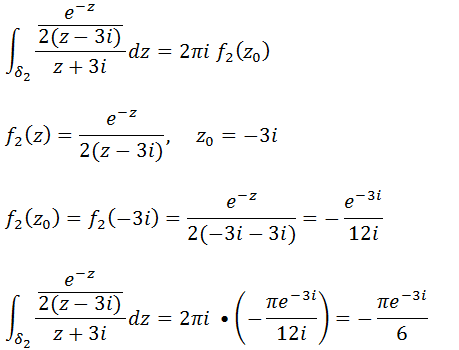
Vamos somas os resultados da integral 1 e integral 2 para achar resultado final da nossa integral.
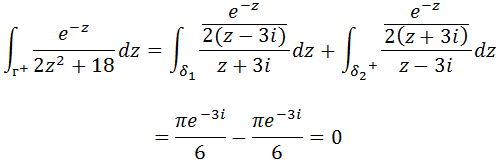
Calcule a integral
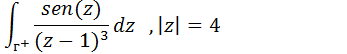
Comparando a nossa forma com a forma da integral de Cauchy podemos notar que;
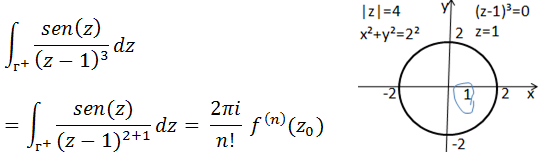
Comparando com o terceiro teorema da integral de Cauchy podemos concluir que;
n=2 ,z₀=1, f(x)=zsen(z)
f(z)=sen(z)
f'(z)=cos(z)
f” (z)=-sen(z)
f”(z₀ )=f”(1)=-sen(1)
Vamos substituir esses resultados na nossa expressão da integral de modo a obter o resultados.
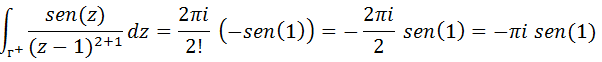
Calcule a integral com г ; |z+2|=9
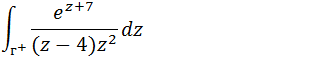
Comparando a nossa forma com a forma da integral de Cauchy podemos notar que;
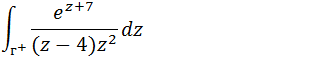
Vamos achar os zeros do denominador e representar a região(z-4)z²=0
z-4=0 ou z²=0
z=4 ou z=0
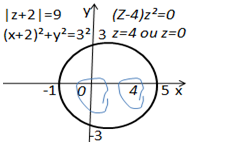
Como temos dois zeros Vamos dividir a região em duas partes
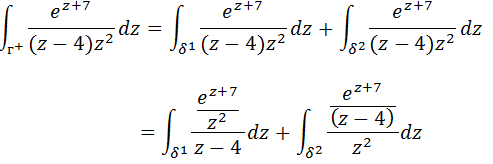
Agora vamos calcular a integral da primeira região
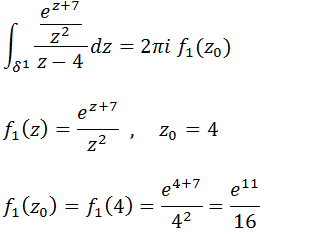
Agora vamos substituir esses resultados na expressão da nossa integral 1.
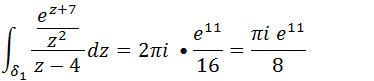
Vamos agora achar a Integral da segunda região
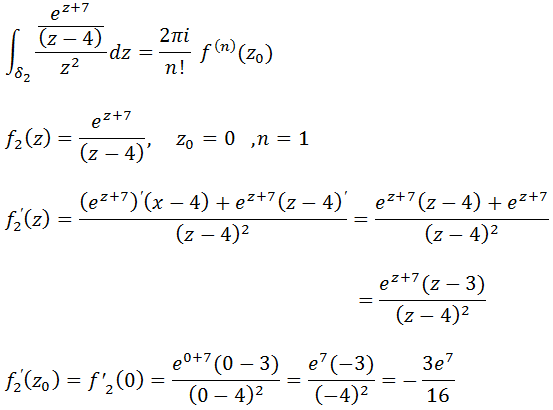
Agora vamos substituir esses resultados na expressão da nossa integral 2.
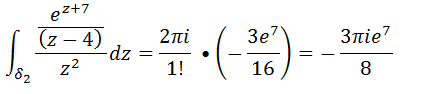
Para achar o resultado da nossa integral vamos somas os resultados da integral 1 e 2.
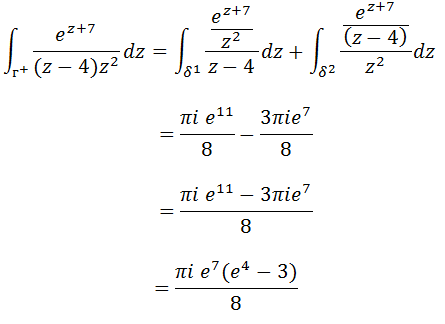
Exercícios para praticar integrais de contorno
Calcule as seguintes integrais
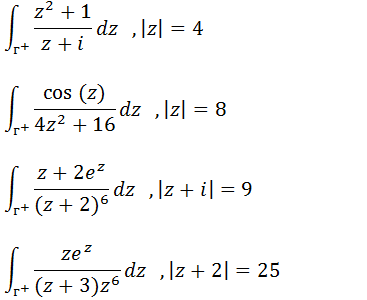
Veja a aula mais uma aula
Equação diferencial com variáveis separáveis
O que são equações diferencial com variáveis separáveis? Equação diferencial com variáveis sepa…
Curso de cálculo de Limites online
Informação sobre o curso O curso é destinados a todos que queiram aprender cálculo de lim…
Calculadora Casio fx-991 MS
Maquina cientifica Casio fx-991 MS Temos disponível calculadora cientifica Casio fx-991 MS, este é u…
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Livro de calculo integral
Livro de calculo Integral Caso você queira aprender calculo integral recomendamos a você adquirir o …
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…

